Κοσμολογία και Κβαντομηχανική!

Λοιπόν με ένα μικρό googlάρισμα βρήκα ότι οι έννοιες αυτές έχουν νόημα στα σύνολα. Όπου αριθμήσιμο απειροσύνολο είναι αυτό το σύνολο που μπορεί να έχει 1-1 αντιστοίχηση με το (απειρο)σύνολο των φυσικών αριθμών.

http://www.softlab.ntua.gr/~fotakis/discrete_math/data/03_Diagonalization.pdf
 
Maestro said:
Λοιπόν με ένα μικρό googlάρισμα βρήκα ότι οι έννοιες αυτές έχουν νόημα στα σύνολα. Όπου αριθμήσιμο απειροσύνολο είναι αυτό το σύνολο που μπορεί να έχει 1-1 αντιστοίχηση με το (απειρο)σύνολο των φυσικών αριθμών.

http://www.softlab.ntua.gr/~fotakis/discrete_math/data/03_Diagonalization.pdf
Click to expand...

Ναι αλλα κατι λεει και για πραγματικους αριθμους που ΔΕΝ μπορεις να ορισεις το πληθος αναμεσα στο 0 και 1
(χωρις να το παιζω γκουρου ...)
 
Last edited:
Λοιπον,
για να μην αφηνουμε εκκρεμοτητες γυρω απο τα απειρα δεκαδικα ψηφια του 1/3 (στιχομυθια nbullamatsis και chrisssb)
εχω την εντυπωση, οτι η σωστη περιγραφη της προοδου ειναι = (3 / 10) + (3 / 100) + (3 / 1000) + 3 / (10000) + ...
ΔΗΛΑΔΗ, 0.3 + 0.03 + 0.003 + 0.0003 + ...

Βεβαια ο Chrisssb (η ο nbullamantsis) ΔΕΝ μιλησαν για προοδο αλλα για ξερα δεκαδικα (0.333333 + 0.333333 + 0.333333 + ...).
Απο την στιγμη που το 1/3 αναλυεται σε μια απειρη γεωμετρικη σειρα τοτε ισχυει ο τυπος S = a / (1 - r), οπου συγκλινει αυτη
η γεωμετρικη σειρα. (ΔΕΝ ΕΙΜΑΙ ΜΑΘΗΜΑΤΙΚΟΣ .... ΑΠΟ ΔΩ ΤΟ ΞΕΤΡΥΠΩΣΑ ... http://www.jimloy.com/algebra/gseriez.htm)

To r υπολογιζεται ως 10^-n, οπου n ειναι το πληθος των ψηφιων της περιοδικοτητας του a (στην περιπτωση μας ... ειναι 1, απο
το 0.3 στο 0.33 στο 0.333 στο 0.3333 και ουτω καθεξης ΟΜΩΣ, αν ο a ηταν 1/7 που ισουται με 0.142857142857142857142857
τοτε το n θα ηταν 6 ... γιατι τοσα δεκαδικα ψηφια χρειαζεται για να επαναληφθει το 142857.)

Αρα .... αν παρω το a = 0.3 που ειναι ο περιοδικος αριθμος και το r = 0.1 την περιοδικοτητα του
εχω ολα οσα χρειαζομαι για να ξαναβρεθω πισω στην αγκαλια και σιγουρια του 1/3 (και οχι του 0.33333333 ....)

a / (1 - r) = 0.3 / (1 - 0.1) = 0.3 / 0.9 = 1/3 !!!!!!!!






(βαρατε βιολιτζηδες τωρα ..... σαπιστε με στο ξυλο ..... :laugh: ..... τολμησα να σηκωσω κεφαλι ο αγεωμετρητος !)
 
Physicists To Test If Universe Is A Computer Simulation

Physicists have devised a new experiment to test if the universe is a computer.

A philosophical thought experiment has long held that it is more likely than not that we're living inside a machine.

The theory basically goes that any civilisation which could evolve to a 'post-human' stage would almost certainly learn to run simulations on the scale of a universe. And that given the size of reality - billions of worlds, around billions of suns - it is fairly likely that if this is possible, it has already happened.

And if it has? Well, then the statistical likelihood is that we're located somewhere in that chain of simulations within simulations. The alternative - that we're the first civilisation, in the first universe - is virtually (no pun intended) absurd.

And it's not just theory. We previously reported that researchers at the University of Bonn in Germany had found evidence the Matrix was less than fiction. That story was by far our most popular of the year - indicating it's something about which you lot have wondered too.

http://www.huffingtonpost.co.uk/201...2745.html?utm_hp_ref=fb&src=sp&comm_ref=false
 
Άν αυτο το "πείραμα" είχε τολμήσει κάποιος να το διανοηθεί και να το εκστομίσει είκοσι χρόνια πρίν,η ακαδημαϊκή του καριέρα θα είχε καταστραφεί αυτοστιγμεί.Μπαίνουμε σε μιά νέα θαυμαστή εποχή για την επιστήμη,και ειδικά για τη Φυσική κύριοι,επειδή ακριβώςτα νοητικά άλματα και η φαντασία δε σκοντάφτουν πλέον σε αγκυλώσεις επιστημονικών "τζακιών".Και ας ενίσταται ο φίλος NikosGX..Όταν η επιστημονική σκέψη πετάξει μακρυά από το πατρονάρισμα και τον αυστηρό φορμαλισμό που την οδηγούν εκ του ασφαλούς,τότε θα ξεκινήσει η ερμηνεία του Κόσμου....
 
Το συμπαν δειχνει να ειναι μια μορφογενετικη δομη (Turing machine) αλλα με μια πολυπλοκοτητα που συντριβει.
Το "μυαλο του θεου", οπως λενε οι Αγγλοσαξονες σεναριογραφοι. ΟΜΩΣ ... αλλο πραγμα να το φανταζεσαι και
τελειως ΑΛΛΗ ιστορια να το αποδεικνυεις. Πολυ περισσοτερο δε να το δημιουργεις ! Εκτιμηση μου (αγεωμετρητη)
ειναι οτι χρειαζομαστε ΕΞΩΠΡΑΓΜΑΤΙΚΕΣ ενεργειες που ειναι ταξεις μεγεθους πανω απο τα 14 TeV του CERN.
Καποιοι εικαζουν οτι ΟΥΤΕ η περιμετρος του γαλαξια δεν φτανει για να αποδεσμευτουν ενεργειες κβαντικων
διακυμανσεων που θα ειναι αρκετα ισχυρες ωστε να γεννησουν ενα καινουργιο συμπαν (περιπου οπως προεκυψε
το δικο μας).

Ομως .... το προβλημα δεν σταματαει στις ενεργειες !!!!

Σκεφτομαστε σαν τον Χριστοφορο Κολομβο που σκεφτεται ποσες θαλλασες, καραβια και ανεμους χρειαζεται
για να φτασει στο φεγγαρι. Η ποσα καψουλια μεσα σε εναν Κρονο-5 θα μας εκσφενδονισουν εκει ...... εξω.
ΔΕΝ ΠΑΕΙ ΕΤΣΙ !!!! Η μονη "ενεργεια" που θα μας παει "εκει" (οπουδηποτε) ειναι η αντισυμβατικοτητα σκεψης
μαζι με εναν σκασμο χρονια (πολυ περισσοτερα απο μερικους αιωνες). Γιαυτο ειναι εξαιρετικα σημαντικο, ΤΩΡΑ
που αρχισαμε να οσμιζομαστε το μεγαλειο του ΟΝΤΟΣ, να μην αυτοκαταστραφουμε σε μια εκρηξη υπεροψιας
και απεραντης επαρσης. Το σημειο Μηδεν της πιθανης αυτοκαταστροφης οπου καθε πολιτισμος πρεπει να
δωσει εξετασεις (κατα Francis Drake).

Και με αυτα που βλεπω στο Youtube με τους λεονταρισμους της Βορειας Κορεας αλλα και την παγερα ειρωνικη
σταση των "μεγαλων" και "σοφοτερων" ..... ΔΕΝ ΕΙΝΑΙ ΚΑΘΟΛΟΥ ΣΙΓΟΥΡΟ ΟΤΙ ΘΑ ΠΙΟΥΜΕ ΝΕΡΟ ΑΠ'ΤΗΝ ΠΗΓΗ !

Προσωπικα, το σημειο Μηδεν ..... το εντοπιζω στις αρχες του 22ου αιωνα ..... δεν ειναι μονο η Κορεα, ουτε οι ΗΠΑ.
Ειναι αυτος ο καλπασμος του παγκοσμιου πλυθησμου που εχει ξεπερασει τα 7 δις ψυχες ... οταν οι μελετες κραυγα-
ζουν οτι ο πλανητης μπορει να συντηρησει ΜΕΧΡΙ 15-16 δις.

Αυτο το νουμερο .... θα το φτασουμε, καποια στιγμη, στις αρχες του 22ου αιωνα !!!!
Ας οψεται η Ιατρικη προοδος αλλα και ο γιγαντισμος ενεργειακων απαιτησεων ΠΡΩΗΝ υπαναπτυκτων περιοχων.
ΟΛΟΙ ΑΥΤΟΙ (οπως εμεις) ΘΑ ΑΞΙΩΣΟΥΝ ΤΟ ΚΑΤΙΤΙΣ ΤΟΥΣ. Και με το δικιο τους ..... ποιος θα τους ενημερωσει
οτι η πιτα εχει μεγαλωσει δεκα φορες το μεγεθος του ταψιου ????
 
Last edited:
Νικος Πετειναρακης said:
Άν αυτο το "πείραμα" είχε τολμήσει κάποιος να το διανοηθεί και να το εκστομίσει είκοσι χρόνια πρίν,η ακαδημαϊκή του καριέρα θα είχε καταστραφεί αυτοστιγμεί.Μπαίνουμε σε μιά νέα θαυμαστή εποχή για την επιστήμη,και ειδικά για τη Φυσική κύριοι,επειδή ακριβώςτα νοητικά άλματα και η φαντασία δε σκοντάφτουν πλέον σε αγκυλώσεις επιστημονικών "τζακιών".Και ας ενίσταται ο φίλος NikosGX..Όταν η επιστημονική σκέψη πετάξει μακρυά από το πατρονάρισμα και τον αυστηρό φορμαλισμό που την οδηγούν εκ του ασφαλούς,τότε θα ξεκινήσει η ερμηνεία του Κόσμου....
Click to expand...

Οταν λαμπρά μυαλά σαν τον Λέοναρντ Σάσκιν στα 16 τους χρόνια ήταν υδραυλικοί, καταρρίπτονται άμεσα τέτοια "επιχειρήματα".....
 
Ξερεις οτι ο Susskind (και ο Smolin), απο τους πρωτεργατες θεμελιωτες της θεωριας Χορδων ... μιλαει για
αλλαγη παραδειγματος, δηλαδη για εγκαταλειψη της θεωριας ???? ΔΕΝ του αρεσει η Χορδη ... ως παραδειγμα.
Αναζητει αλλο :laugh:

Παντως, δεν γνωριζα οτι εβαλε τα χερια του σε λεκανες .....



(αμα τα βαλω εγω ...... θα βγαλει τιποτα η γκαγκαουκα μου ? ..... χμμμμμ)
 
Last edited:
Το συναρπαστικό είναι οτι μιλάει απο την μία για την απεικόνιση της τρισδιάστατης αντίληψης της πραγματικότητας και απο την άλλη οτι συνυπάρχει με την δισδιάστατη "απεικόνιση" της, ως πληροφορία, στα "τείχη" του σύμπαντος...


Αν σου πω οτι καταλαβαίνω και πολλά βέβαια...θα είναι ψέμα.
 
ΔΕΝ βλεπει το συμπαν σαν μπαλλα, οπου κατι τρισδιαστατο ριχνει δισδιαστατη "σκια" καπου στην εσωτερικη επιφανεια
αυτη της σφαιρας !!! Το συμπαν ειπαμε οτι ΔΕΝ ειναι 3D, και ας ειναι πεπερασμενο (13.7 δις ε.φ. ακτινα ... minimum).

O Susskind (και λοιποι) κατορθωνει και ΝΟΕΙ περα απο το 3D, σε υπερχωρους που ενθυλακωνουν τους απλουστερους
ως ... σκιες (για την ακριβεια, ως προβολες η ιχνη). Με αυτη την προσεγγιση, το υποτιθεμενο τελος του συμπαντος
ισως να περιεχει περισσοτερο "χωρο" για αποθηκευση πληροφοριων απο οτι το κοιλο μιας σφαιρας.
Χωρο υπερδιαστατο σε μικροκλιμακα αλλα σταθερα τρισδιαστατο σε μακροκλιμακα.
 
Last edited:
Απάντηση: Re: Κοσμολογία και Κβαντομηχανική!

chrisssb said:
Physicists To Test If Universe Is A Computer Simulation

Physicists have devised a new experiment to test if the universe is a computer.

A philosophical thought experiment has long held that it is more likely than not that we're living inside a machine.

The theory basically goes that any civilisation which could evolve to a 'post-human' stage would almost certainly learn to run simulations on the scale of a universe. And that given the size of reality - billions of worlds, around billions of suns - it is fairly likely that if this is possible, it has already happened.

And if it has? Well, then the statistical likelihood is that we're located somewhere in that chain of simulations within simulations. The alternative - that we're the first civilisation, in the first universe - is virtually (no pun intended) absurd.

And it's not just theory. We previously reported that researchers at the University of Bonn in Germany had found evidence the Matrix was less than fiction. That story was by far our most popular of the year - indicating it's something about which you lot have wondered too.

http://www.huffingtonpost.co.uk/201...2745.html?utm_hp_ref=fb&src=sp&comm_ref=false
Click to expand...

Eλπίζω να μην τρέξουν κανα antivirus και προπαντώς μη γίνει κανα reboot...
 
Άλλο ένα πείραμα που πήγε λάθος ή τελικά κάτι μας διαφεύγει που έχει σχέση με τη μάζα του πρωτονίου?
Δοκιμάζοντας μια νέα πειραματική τεχνική επιστήμονες προσπάθησαν να υπολογίσουν με το νέο τρόπο τη μάζα του πρωτονίου – και τη βρήκαν 4% μικρότερη.
Λάθος στους υπολογισμούς? Λάθος στο μοντέλο ? Όλα είναι πιθανά.

http://news.discovery.com/space/proton-mass-mystery-130415.htm
 
Ο Τζιπασχας ποσταρε κατι παρομοιο στο post #191 ...
Ειμαι περιεργος ομως .... γιατι 4% στην εκτιμηση του αρχικου ογκου .... θεωρειται τοσο κοσμοιστορικη διαφορα ?
Υποθετω οτι με την αλλαγη της μεθοδου (βλεπε, μυονια) ο υπολογισμος εγινε ακριβεστερος (απο οτι με ηλεκτρονια).
 
Ας προχωρησουμε with Lesson 101 ... της θεωριας Χορδων (και ας την εγκαταλειπουν σιγα-σιγα ... οι πρωτεργατες)

Στο προηγουμενο "μαθημα" ειδαμε ποση σημασια εχει η Κλιμακα (για την συγκαλυψη-πακτωση εξτρα διαστασεων).
Σε αυτο το "μαθημα" (και καλα !!!) θα εξετασουμε γιατι ΧΟΡΔΗ και οχι ΣΗΜΕΙΟ. Τι παραπανω εχει μια Χορδη ?

Ενας τομεας που η Χορδη υπερτερει (γεωμετρικα) ειναι .... η ΚΑΜΠΥΛΩΣΗ και κατ'επεκταση η ΣΥΣΤΡΟΦΗ.
Αντιστοιχα, το Σημειο δεν μπορει να δωσει αυτη την πολυτελεια (ουτε καν ... η ακαμπτη Ευθεια).
Ας ξεκινησουμε απο μια ΚΛΕΙΣΤΗ Χορδη, και τι τελειοτερο και συμμετρικοτερο απο εναν κυκλο !
Ξεκιναω απο το παραδειγμα του κυκλου για να φτασουμε χαλαρα και ξεκουραστα στον ... ΒΡΟΓΧΟ !

Τι μπορει να κανει, λοιπον, ενας κυκλος οταν .... "κυμματισει" ?
Σε πρωτη φαση (και μονο πανω στο επιπεδο) .... αυτο :


Image 01.png


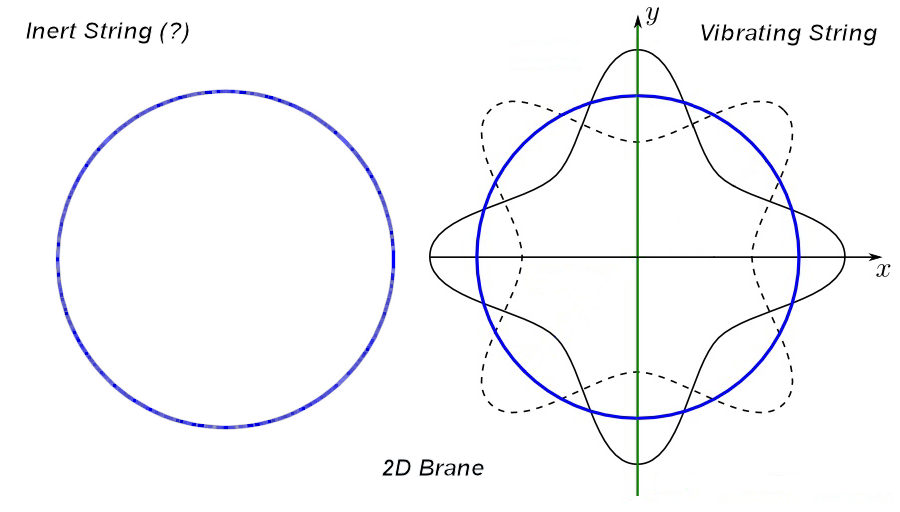
Oμορφο το παραδειγμα .... αλλα κατι του λειπει .... χμμμμμ ....
Μηπως να ξεφευγαμε λιγακι απο την Κυκλικοτητα και να πηγαιναμε στην Ελλειπτικοτητα ?
Και μαλιστα ανεπτυγμενη στο μηκος του Χρονου ? ..... ας την δουμε :


Image 02.jpg


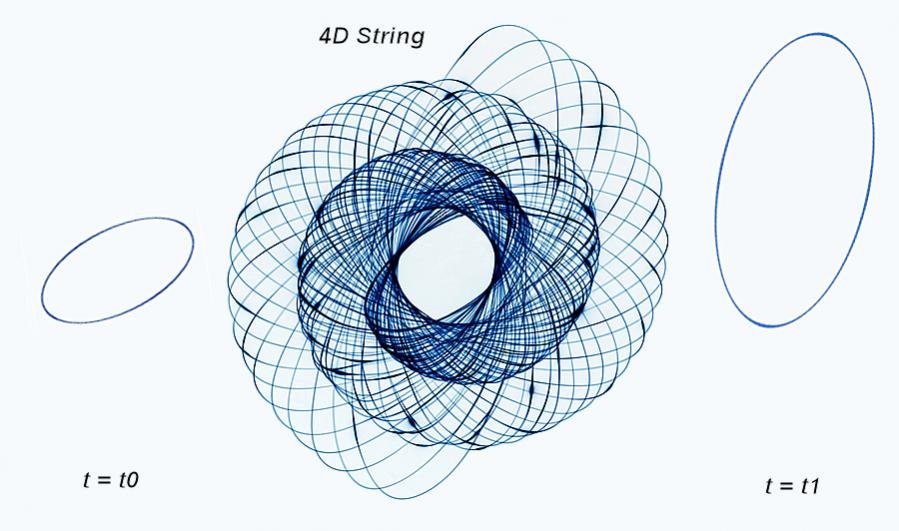
Ωραια ... μια Ελλειψη περιστρεφομενη και τανυσμενη μπορει να μας δωσει μια ισχνη μυρωδια
για το πολυδιαστατο μιας Χορδης. ΟΜΩΣ, μην ξεχναμε οτι ΑΚΟΜΑ βρισκομαστε ... στις 4 διαστασεις.
Και οχι στις 10 .... Aς δουμε, περα απο τους "κυμματισμους" του κυκλου και μερικες συστροφες του :


Image 03.png


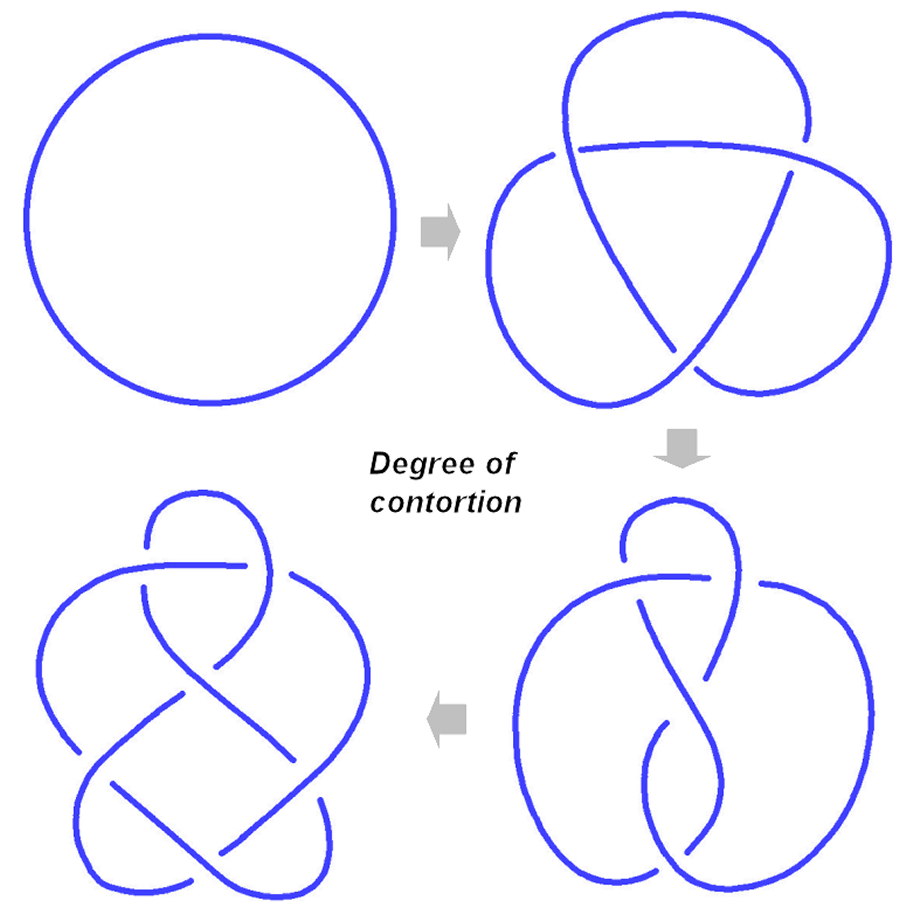
Αν λοιπον, μια Χορδη μπορει να τεντωσει και να συστραφει, τοτε ... ορεξη να χουμε για ΚΟΜΠΟΥΣ :laugh:.


Image 04.jpg


Kαι μερικους κομπους ... μεταξυ διαφορετικης συχνοτητας βρογχων (με πρασινο και μπλε χρωμα).


Image 05.jpg


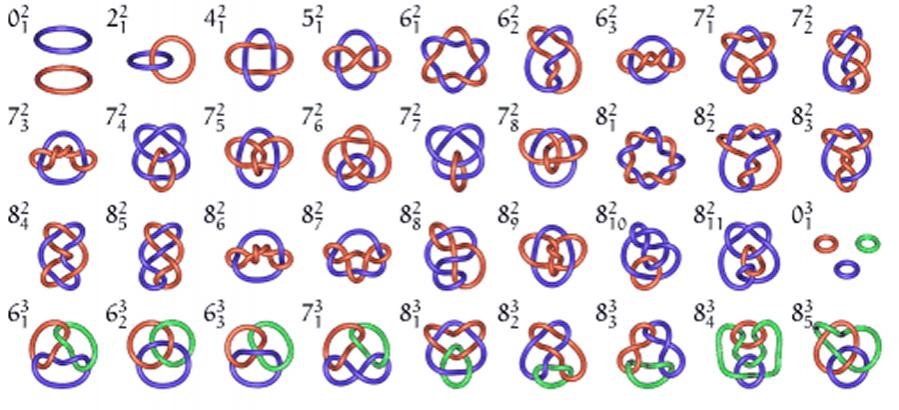
Επομενως, ο Κυκλος ειναι υπερβολικα συμμετρικος για την ποικιλομορφια και χρηστικοτητα ενος Βρογχου
και ιδιως ενος κλειστου Βρογχου. Μαλλον, αρχιζουμε να φτανουμε σε πιο συνθετα σχηματα (ενορασεις) ενος
Παλλομενου Βρογχου. Α ΝΑΙ ... ξεχασα .... καθε Χορδη ΠΑΛΛΕΤΑΙ, αλλιως δεν προσφερει ιδιαιτερη ευελιξια.


Image 06.png


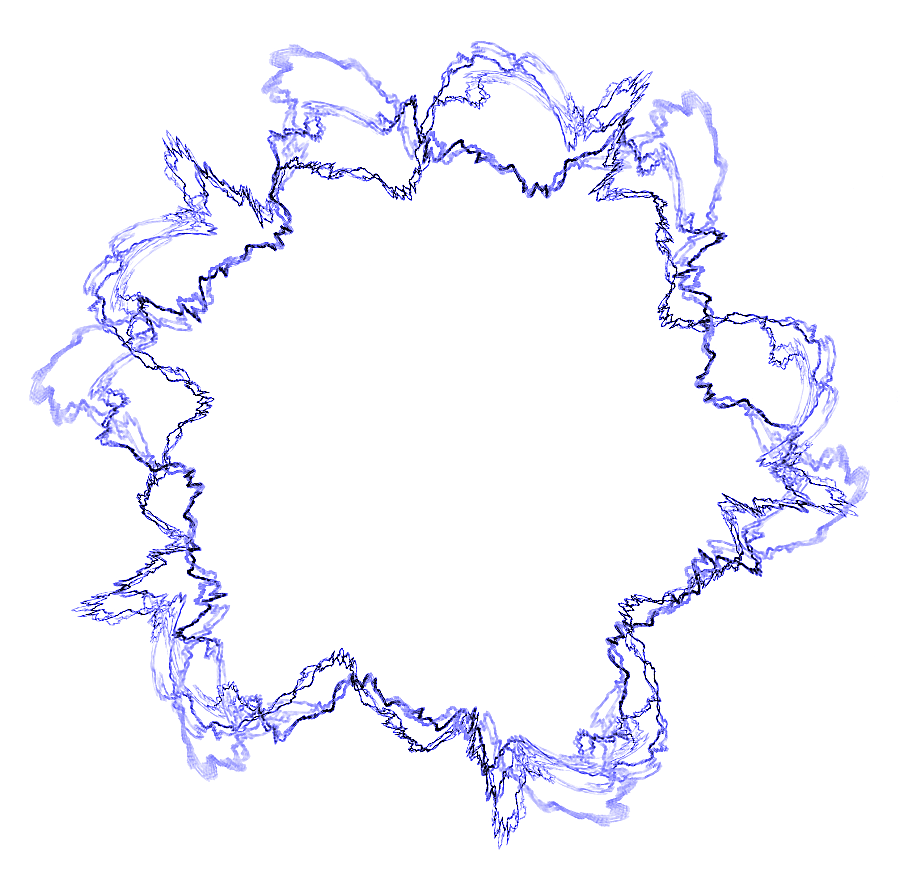
Το παραπανω σχημα , ομως , ειναι ΜΙΑ χορδη (παντα κλειστη). ΤΙ γινεται οταν αρχιζουν να διαπλεκονται ΠΟΛΛΕΣ
μεταξυ τους (ΟΧΙ μονο μιας συχνοτητας χορδες, ουτε μονο κλειστες χορδες) ???? Ε .... το πραγμα κουβαριαζεται και
τσουβαλιαζεται (ασυστολα) :laugh: Kαι δεν φαινεται ξεκαθαρα τι ειναι συμμετρικο (μια συχνοτητα + τις αρμονικες της)
και τι ασυμμετρο (ΟΛΕΣ οι συχνοτητες + ΟΛΕΣ οι αρμονικες + Ανοιχτοι Βρογχοι + Κλειστοι Βρογχοι ... ΤΑ ΠΑΝΤΑ ΟΛΑ).


Image 07.jpg


Προσεξτε κατι αλλο τωρα .....
Ειπαμε οτι καθε Χορδη ΠΑΛΛΕΤΑΙ, περιπου σαν την χορδη μιας κιθαρας. Ομως, οι χορδες μια κιθαρας ΔΕΝ παλλονται ολες
ΟΥΤΕ με το ιδιο πλατος ΟΥΤΕ με το ιδιο υψος ταλλαντωσης. Ετσι δεν ειναι ? Το τελευταιο πραγμα που θα περιμεναμε να
δουμε σε ενα πληθος χορδων ειναι να παλλονται συγχρονισμενα ... καπως ετσι :


Image 08.jpg


Mαλλον, ειναι πολυ πιο ρεαλιστικο να εικασουμε οτι Χορδες διαφορων συχνοτητων (δηλαδη, ενεργειων) ΔΕΝ συγχρο-
νιζονται ΠΛΗΝ ελαχιστων εξαιρεσεων (που οντως συγχρονιζονται, αλλα δεν ειναι του παροντος να αναλυσουμε).
Ο ασυγχρονισμος πρεπει να θεωρειται ΔΕΔΟΜΕΝΟΣ ....


Image 09.jpg


Εαν δεν ηταν ΗΔΗ κουβαρι το μυαλουδακι σας, μετα απο ολα αυτα ... ακουστε και αυτο : μια ομαδα Χορδων
μπορει να δειχνει απο "μακρια" οτι ειναι μια Χορδη ενω ειναι .... καμποσες ξεχωριστες. Προσεξτε, οι Χορδες
δεν εχουν διαφορα "παχη". ΕΝΑ ΠΑΧΟΣ εχουν (απο οσο εχω ψαξει τουλαχιστον) και ειναι της κλιμακας
10^-34 του μετρου (λιγο πανω απο το οριο Planck). Απλα, μπορουν να συγχρονιστουν και να δειχνουν
σε μια μεγαλυτερη κλιμακα ως ΕΝΑ ΣΤΑΣΙΜΟ ΚΥΜΑ .... ομως αν πλησιασουμε κοντυτερα ενδεχεται
να αναλυονται σε καμποσα μικροτερα κυματα (που αντιστοιχουν σε πραγματικες χορδες).


Image 10.jpg


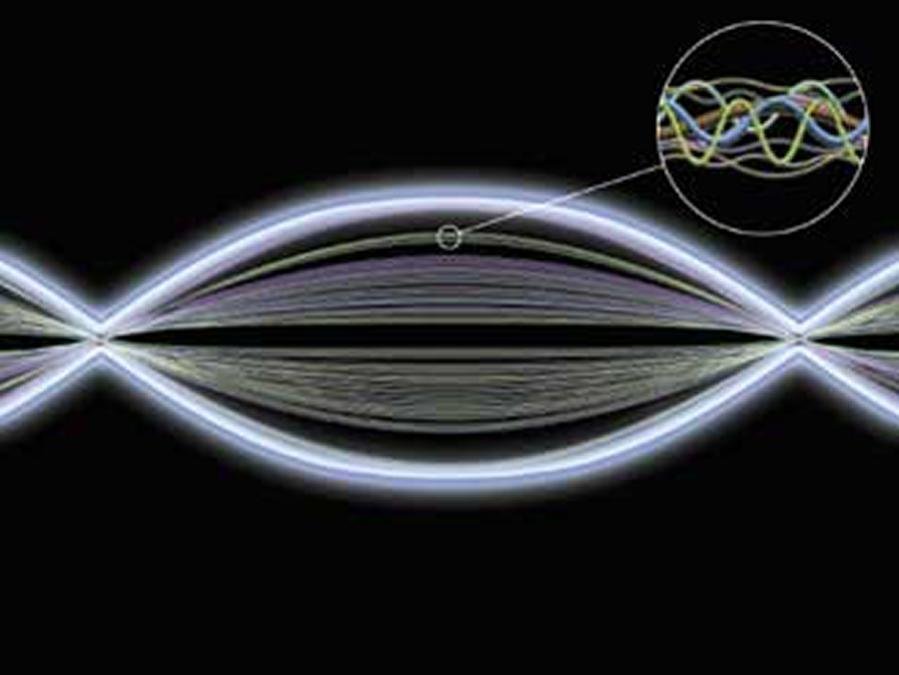
(και ΔΕΝ εχουμε φτασει ΚΑΝ .... στην τεραστια διαφορα μιας Ανοιχτης και Κλειστης Χορδης .... χοχοχοχοχο)
 
Last edited:
Ρε συ "δάσκαλε", εκτός αν έχασα εγώ κάποιο μάθημα και τα είπες εκεί, δεν έκανες την εισαγωγή για όσους δεν έχουν ασχοληθεί καθόλου με το θέμα (καλά οι γνώστες που τα γνωρίζουν από χρόνια και σε μεγαλύτερο βάθος). Πως σύμφωνα με τη θεωρία αυτή, τα σωματίδια της Φυσικής δεν είναι ...μπαλάκια απειροελάχιστου μεγέθους, σημεία, που γυρίζουν το ένα γύρω από το άλλο ή συγκρούονται μεταξύ τους σαν μικροσκοπικό μπιλιάρδο, αλλά "νήματα" απειροελάχιστου πάχους, μίας διάστασης, τα οποία "πάλλονται" σαν χορδές και των οποίων οι φυσικές ιδιότητες, όπως η μάζα, είναι αποτέλεσμα του είδους και της συχνότητας της ταλάντωσης αυτής, παραδείγματα των οποίων υπάρχουν στα όμορφα σχέδια που παρέθεσες. Νομίζω πως πρέπει να ξεκινήσεις από εκεί, γιατί φαντάζομαι θα αναφερθείς αργότερα και στις -βράνες :)
 
ΕΠΙΤΗΔΕΣ δεν ξεκινησα απο κει !!!!

Πιανω το ολο ζητημα ΓΕΩΜΕΤΡΙΚΑ και μονο ΓΕΩΜΕΤΡΙΚΑ ... οπου οι περισσοτεροι εχουν μια καποια τριβη.
Αν πιασω το θεμα απο τα "μπαλακια απειροελαχιστου μεγεθους" ... ΠΩΣ θα εξηγησω οτι ΔΕΝ ειναι τρισδιαστατα μπαλλακια ?

Ε ? ....... :laugh:


(μην μου τους κυκλους ταραττε .... :flipout:.... βιαστικοι και σχετικοι και ενθουσιωδεις συνοδοιποροι μου -bye-)
 
Last edited:
http://prl.aps.org/abstract/PRL/v110/i16/e168702
Casual Entropic Forces

Μια ακόμα προσπάθεια σύνδεσης της νοημοσύνης με την εντροπία και τη θερμοδυναμική…
http://www.insidescience.org/content/physicist-proposes-new-way-think-about-intelligence/987

"[The paper] is basically an attempt to describe intelligence as a fundamentally thermodynamic process,"
The universe exists in the present state that it has right now. It can go off in lots of different directions. My proposal is that intelligence is a process that attempts to capture future histories," said Wissner-Gross.
 
Top Bottom